R-Tree Indexes
As explained in the Indexes page, the eXtremeDB
rtreeindex is commonly used to speed spatial searches; for example, find the rectangle that contains this point, find all rectangles that overlap this rectangle, or find all rectangles in the neighborhood of this point.All manner of shapes can be stored and searched with the
rtreeindex. For example, a point is represented as a rectangle with width and height = 1 and a line that has starting and ending coordinates of 15, 844 and 0, 3647 is stored as rectangle with its upper left corner at 15, 844 and its lower right corner at 0, 3647.To determine if two lines intersect, or if a point is within a given area (described by a circle, rectangle, etc.), an
rtreesearch is performed to find all overlapping rectangles. For each match, a further test is conducted in the application code to determine whether the condition is actually met.For example, consider that we have lines as follows:

A search to discover all lines that intersect with (75, 15) (20, 70) would return the rectangle bounding (35, 25) (20, 30) because the rectangles overlap. The application would extract additional information for the object, for example, that it is a line and what its starting and ending coordinates are, and would conclude that this line does not intersect the key line; and would continue to the next overlapping rectangle returned by the index search.
Note that, any shape with coordinates {(X1, Y1), (X2, Y2), ... (Xn, Yn)} can be stored and searched in this manner. For example, consider a polygon:
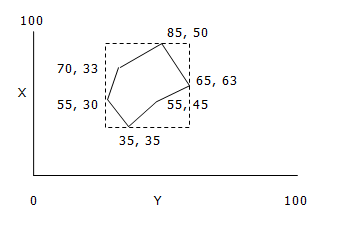
Here the X coordinates are
35, 55, 65, 70, 85and Y coordinates are30, 33, 35, 45, 50, 63. The bounding rectangle is the rectangle with left top vertex (Xmax,Ymin), and right bottom vertex (Xmin, Ymax) where Xmin = min(Xi), Ymin=min(Yi), Xmax = max(Xi), Ymax=max(Yi). In this case, Xmax =85, Ymin =30, Xmin =35, Ymax =63and our rectangle top left and bottom right is(85, 30)and(35, 63).
rtreesearches can return rectangles that:1) exactly match the given coordinates,
2) overlap the given coordinates,
3) wholly contain the given coordinates, or
4) are sorted in order of their distance from a specified reference rectangle or point.
Though rectangle coordinates may be specified in different ways, for example as the two points corresponding to the top left and bottom right, for
rtreeindexes the rectangles must be specified as arrays of max and min coordinates. For example, a two-dimensional rectangle is represented as an array:xMin,yMin,xMax,yMaxIn other words, using X and Y coordinates as diagrammed above, the
<xMin, yMin>coordinates correspond with the lower left point while<xMax, yMax>is the upper right point. A three-dimensional “rectangle” is represented as follows:xMin,yMin,zMin,xMax,yMax,zMaxExample R-Tree Search
To demonstrate
rtreeindex usage, consider the rectangles and point in the diagram below:
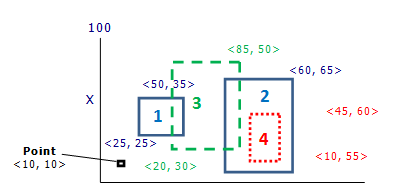
The two solid lined rectangles are defined by coordinates
<25,25> - <50,35>and<5,45> - <60,65>., the dash-lined rectangles by<20,30> - <85,50>and<45,60> - <10,55>.To store these rectangles in a database, we might create a class Boxes with an
rtreeindex like the following:class Boxes { int2 square[4]; rtree <square> ridx; };Then we would insert the four rectangles using the API of choice.
The
rtreeindex allows four types of search operations: equals, contains, overlaps or neighborhood.To perform an
rtreesearch, as with other index types, acursormust first be created. Then, to search the database for a specific rectangle, we would perform acursorsearch operation with operation type equals specifying the rectangle (four coordinates) of interest.To search for rectangles that overlap a specified rectangle the overlaps operation type is used. For example, a search for the dash-lined rectangle number 3 (
<20,30> - <85,50>) in the diagram would “find” the two solid lined rectangles 1 and 2.Similarly, to search for rectangles that contain a specified rectangle the contains operation type is used. For example, a search for the dot-lined rectangle number 4 (
<45,60> - <10,55>would “find” only the larger solid lined rectangle number 2 (<5,45> - <60,65>).Using the neighborhood operation type will return all rectangles in the index ordered by their distance from the specified rectangle or point. (Note that a point can be specified as either a two-dimensional array of coordinates or as a “degenerate rectangle” where the lower-left and upper-right coordinate values are identical. Though the internal search algorithms, particlularly for overlaps and contains operation types, deal with “boxes”, promoting points to rectangles, in some cases the memory requirements are significantly less for storing points rather than rectangles.)
In the current example specifying the point
<10,10>would return all four inserted rectangles ordered from left to right because the specified point is to the left of each. This search calculates the Euclidean distance from the lower-left (minX, minY) point of the target rectangle (<10,10>in this case) to the closest point in each rectangle in the index and returns the results in order from smallest to largest distance.
Note that an
rtreeindexcursorhas different semantics than a conventionaltree(B-Tree) type cursor. Whereas, the search operation of a conventionaltreeindex positions the cursor at the first match, or just before the nearest match in the case of a partial key search, thertreeindex cursor operates on the result set of the search. In other words, for anrtree cursor, the cursor operations first, last, next and prev operate within the set of objects that match the given search conditions.